Prototyping a Small Genetic Algorithms Library in Haskell
This post assumes a basic understanding of genetic algorithms and the terminology associated with them, as well as a cursory understanding of recursion schemes; resources for both may be found scattered within the post. All source code can be found here.
First blog post – yay! This post documents some of my experience getting practice with recursion schemes and some monadic computations in the context of prototyping a genetic algorithms library. For a full-fledged, flexible, genetic algorithms library written in Haskell, I refer the reader to moo.
Getting a birds-eye view
Genetic algorithms are a type of heuristic in which candidate solutions to a problem are stochastically and incrementally evolved over time with the aim of producing performant ones; candidates, or individuals, are evolved with the help of genetic operators for selecting, manufacturing, and altering those individuals.
Contextualizing the computations
Let’s start by defining some of the context in which our genetic
algorithm should run. It would be nice to reference a configuration
containing all the definitions and parameters we could need (like
mutation
and
selection
methods), utilize and update a random number generator for generating
and mutating individuals, and log intermediate data. The
RWS
monad presents itself as a candidate for meeting these criteria, so
let’s wrap it in a newtype:
newtype GAContext indv a = GAContext {
ctx :: RWS (GAConfig indv) [T.Text] PureMT a
} deriving (
Functor,
Applicative,
Monad,
MonadReader (GAConfig indv),
MonadWriter [T.Text],
MonadState PureMT
)With this definition (which requires GeneralizedNewtypeDeriving), we
can reference and update the
PureMT
random number generator with get and
put,
refer to our configuration with
ask,
and log intermediate data with
tell.
Gathering intermediate data
One of my favorite genetic algorithm libraries, deap, allows you to keep track of a hall of fame – a collection of the most-fit individuals. We can represent this collection as a continually-updated min-heap, where the worst-performing individuals at a particular point in time can be popped from the heap and discarded:
import qualified Data.Heap as Heap
type HOF a = Heap.MinHeap aIt would be helpful to have a means of tracking the best individuals over time, along with any other data that could be gathered with every new generation. For this, a snapshot data type:
data GASnapshot a = Snapshot {
-- the collection of individuals from the last generation
lastGeneration :: Vector a
-- the collection of top performers, the Hall of Fame (HOF)
, hof :: HOF a
-- the current generation id
, generationNumber :: Int
} deriving (Show)Configuring the genetic algorithm
Next we can define the data type containing all of our configuration
parameters that we will then be able to reference in GAContext
computations:
data GAConfig i = Config {
-- the probability an individual is mutated
mutationRateInd :: Double
-- the probability a gene of an individual is mutated
, mutationRateGene :: Double
-- the percentage of the population that gets replaced through recombination
, crossoverRate :: Double
-- the population size
, popSize :: Int
-- the mutation method
, mutate :: i -> GAContext i i
-- the crossover method
, crossover :: i -> i -> GAContext i i
-- the method to create a new individual
, randomIndividual :: GAContext i i
-- the selection method
, selectionMethod :: Vector i -> GAContext i (Vector i)
-- the fitness function (higher fitness is preferred)
, fitness :: i -> Double
-- the number of generations
, numGenerations :: Int
-- the `hofSize` best individuals across all generations
, hofSize :: Int
-- function for information sourced from most recent snapshot
, logFunc :: GASnapshot i -> GAContext i ()
}This configuration serves as the basic interface to the library. Once an instance of this data type is created, the genetic algorithm can do the bulk of its work.
Utilizing the genetic operators
The genetic algorithm will evolve our set of candidate solutions over time for a fixed number of steps, or generations.
Grabbing snapshots
Every generation of the genetic algorithm is determined by a step
function:
step :: Ord a => GASnapshot a -> GAContext a (GASnapshot a)
step (Snapshot lastGen hof genNumber) = do
Config {hofSize, logFunc, popSize, selectionMethod} <- ask
-- select parents and create the next generation from them
selectedParents <- selectionMethod lastGen
-- use the set of parents to create and mutate a new generation
children <- crossAndMutate selectedParents popSize
-- update the HOF
updatedHOF <- updateHOF hof children hofSize
-- construct the new snapshot
let nextSnapshot = Snapshot{
lastGeneration = children,
hof = updatedHOF,
generationNumber = genNumber + 1
}
-- log intermediate results
logFunc nextSnapshot
-- return the mutated generation
return nextSnapshotThe step function takes the current snapshot, along with the
user-defined configuration to select a portion of the population to pass
genetic material,
crossover
individuals from that subset to generate children, and mutate a portion
of those children. With every pass, the Hall of Fame is updated with
better-fit individuals, if they are found, and the subsequent snapshot
is returned.
Crossover and Mutation
After parents are selected with the user-defined selectionMethod, the
Vector of parents act as a seed from which children are produced. The
generation of these children via crossover and their mutation are done
in the same pass with a hylomorphism:
-- repeatedly selects two new parents from `parents` from
-- which `n` total children are produced
crossAndMutate :: (Vector a) -> Int -> GAContext a (Vector a)
crossAndMutate parents n = hyloM toVector (newChild parents) nAt this point, I refer the reader to the existing (and superior) resources on recursion schemes, if they are unfamiliar with the concept; I found Awesome Recursion Schemes to be helpful, particularly Patrick Thompson’s series and Jared Tobin’s blog posts.
Briefly, and skipping over useful generalizations provided by the
recursion-schemes
library: catamorphisms tear down structures, anamorphisms construct
structures, and hylomorphisms are the composition of an anamorphism and
a catamorphism, i.e. the construction and tearing-down of an
intermediate structure. Catamorphisms utilize a function to tear down
their structures while anamorphisms utilize a function to build up their
structures. Both functions can be found within
Control.Functor.Algebra
and are representations of the morphisms that each comprise a third of
an
F-Algebra
and F-CoAlgebra
respectively:
type Algebra f a = f a -> a
type CoAlgebra f a = a -> f aNormal hylomorphisms have the type:
hylo :: Functor f => (Algebra f b) -> (CoAlgebra f a) -> a -> b For our case, the monadic context of GAContext needs to be preserved.
The haskell package
data-fix
offers the hyloM function, which instead relies on the monadic
AlgebraM and CoAlgebraM types:
type AlgebraM m f a = f a -> m a
type CoAlgebraM m f a = a -> m (f a)
hyloM :: (Functor f, Monad m) => (AlgebraM m f b) ->
(CoAlgebraM m f a) -> a -> m b With the monadic hylomorphism in crossAndMutate above, a fixed list of
mutated children is unfolded from a seed using newChild and folded
into a vector of the same type using toVector. This yields the next
generation of candidate solutions for the genetic algorithm.
Let’s take a look at the newChild function:
-- selects two parents to breed, a child is born, joy to the world
newChild :: (Vector a) -> CoAlgebraM (GAContext a) (ListF a) Int
newChild parents 0 = return Nil
newChild parents m = do
-- get mutation and crossover methods
Config {crossover, mutate} <- ask
-- get two random indices
i <- randomI
j <- randomI
-- from the two indices, grab two parents
let p1 = parents ! (i `mod` (length parents))
let p2 = parents ! (j `mod` (length parents))
-- make a child
child <- crossover p1 p2
-- mutate the child
mutatedChild <- mutate child
-- add the child to the collection
return $ Cons mutatedChild (m-1)newChild generates a new individual with the user-defined crossover
function from two parents chosen at random from the group individuals
selected to pass on their genetic material. We then apply the
user-defined mutate function to the child and append that mutated
individual to the in-progress collection of children. This is the
anamorphic half of the hylomorphism.
The catamorphic half of the transformation is accomplished with
toVector below:
-- converts Fix (ListF a) into Vector a
toVector :: AlgebraM (GAContext a) (ListF a) (Vector a)
toVector = return . embedand we can see that it is rather straightfoward, once we make a
Corecursive instance of Vector to leverage the embed function:
type instance Base (Vector a) = ListF a
instance Corecursive (Vector a) where
embed (Cons x xs) = x `V.cons` xs
embed Nil = V.emptyIn addition to the above instance, we will find later on, with our use
of
cata
that defining a Recursive instance of Vector is also necessary:
instance Recursive (Vector a) where
project xs | V.null xs = Nil
| otherwise = Cons (V.head xs) (V.tail xs)Updating the Hall of Fame
Once the collection of mutated children has been returned by
crossAndMutate, we will want to update the Hall of Fame with any
individuals that perform better than the extant individuals therein.
Let’s create a function that will take a vector of individuals and
insert them all into the heap representing the Hall of Fame:
-- inserts elements from a list into a heap
insertHeap :: Ord a => HOF a -> (Vector a) -> HOF a
insertHeap hof = cata insert where
insert Nil = hof
insert (Cons a heap) = Heap.insert a heapSimple enough. Our catamorphism breaks down our Vector into a HOF;
all it needs is the existing one into which we can insert the elements.
With this, we can update the current HOF by dumping the latest
population into it and popping off minimally-fit individuals until the
HOF is back at its original size.
-- updates the HOF by removing the worst-fit individuals from the min-heap
updateHOF :: Ord a => HOF a -> Vector a -> Int -> GAContext a (HOF a)
updateHOF hof pop hofSize = return . Heap.drop n $ oversizedHOF where
-- insert all of the current population
oversizedHOF = insertHeap hof pop
-- drop all but hofSize individuals
n = V.length pop - if Heap.isEmpty hof then hofSize else 0Invoking the Genetic Algorithm
Now that we have outlined the flow of the genetic algorithm, we need to
provide an initial population. For this, we leverage the user-defined
randomIndividual function, provided within the ever-present
GAConfig:
-- creates a vector of random individuals
makePopulation :: Int -> GAContext a (Vector a)
makePopulation s = hyloM toVector addRandomInd s where
-- creates a random individual and adds it to the collection
addRandomInd :: CoAlgebraM (GAContext a) (ListF a) Int
addRandomInd 0 = return Nil
addRandomInd n = do
-- get a new, random individual
ind <- randomIndividual =<< ask
-- add it to the collection
return $ Cons ind (n-1)We now have all pieces necessary for running the genetic algorithm for one complete generation. After some initial setup, we can run for the user-specified number of generations:
runGA :: Ord a => GAContext a (GASnapshot a)
runGA = do
Config {numGenerations, popSize, hofSize} <- ask
-- initialize the population
initialPop <- makePopulation popSize
-- set up the initial Hall of Fame
initialHOF <- updateHOF (Heap.empty :: HOF a) initialPop hofSize
-- set up the initial snapshot
let snapshot = Snapshot {
lastGeneration = initialPop,
hof = initialHOF,
generationNumber = 0
}
-- run the genetic algorithm
runN numGenerations step snapshotUsing our configuration parameters we create an initial snapshot and
pass that to a function that runs the step function for a set number of
iterations equal to the number of generations. Let’s take a look at the
definition of runN:
-- a function reminiscent of iterateM that completes
-- after `n` evaluations, returning the `n`th result
runN :: Monad m => Int -> (a -> m a) -> a -> m a
runN 0 _ a = return a
runN n f a = do
a' <- f a
runN (n-1) f a'it takes a function (in our case step) and applies that function n
times, returning the final result.
Finally, we can run the GAContext, a newtype wrapper for the RWS
monad, with runRWS and evalRWS:
-- from a new rng, run the genetic algorithm
evalGA :: Ord i => GAConfig i -> IO (GASnapshot i, [T.Text])
evalGA cfg = newPureMT >>= (return . evalGASeed cfg)
-- from a user-supplied rng, run the genetic algorithm
evalGASeed :: Ord i => GAConfig i -> PureMT -> (GASnapshot i, [T.Text])
evalGASeed cfg rng = evalRWS (ctx runGA) cfg rng
-- from a user-supplied rng, run the genetic algorithm and return the updated seed
runGASeed :: Ord i => GAConfig i -> PureMT -> (GASnapshot i, PureMT, [T.Text])
runGASeed cfg rng = runRWS (ctx runGA) cfg rngWith this, all the user needs to do is define their genetic operators and fitness functions for their own individual representation, and they should be able to call one of these three functions to run the genetic algorithm.
Using the library
Let’s see an example of it in action with a very simple problem:
maximizing the number of 1’s in a 500-bit binary string. Source can be
found in
BinaryInd.hs.
Representation
We’ll represent the binary string as a list of Bool:
data BinaryInd = BI [Bool] deriving (Show)
instance Eq BinaryInd where
(BI b1) == (BI b2) = b1 == b2Fitness function
We can start simply by defining the fitness function for this individual
representation, which is just the number of True booleans in the list:
-- count the number of `True` bools in the chromosome
score :: BinaryInd -> Double
score (BI bs) = fromIntegral . length . filter id $ bs
instance Ord BinaryInd where
b1 `compare` b2 = (score b1) `compare` (score b2)Random individuals
Next we can define a function to create a new and random bit string of length 500:
-- create an individual, represented by a list, by
-- initializing its elements randomly
new :: GAContext BinaryInd BinaryInd
new = fmap BI $ replicateM 500 randomBoolMutation
We’ll also need to provide a way to mutate our individual:
-- mutate a binary string representation
mutate :: BinaryInd -> GAContext BinaryInd BinaryInd
mutate ind@(BI bs) = do
-- grab individual and gene mutation rates
Config{mutationRateGene, mutationRateInd} <- ask
-- get a random double
indp <- randomD
-- if the value is less than mutation rate for an individual
if indp < mutationRateInd then
-- mutate each bit with `mutationRateGene` probability
fmap BI $ mapM (mutateBool mutationRateGene) bs
else
-- return the unaltered individual
return ind
-- mutate a boolean by flipping it
mutateBool :: Double -> Bool -> GAContext a Bool
mutateBool p x = do
-- get a random double
indp <- randomD
-- determine whether or not to flip the bit
return $ if indp < p then not x else xIn mutate, we get a random double with a helper function randomD and
decide whether the given individual is to be mutated at all. If it is to
be mutated, iterate over the given individual and determine whether the
genes themselves (the bits) should be mutated with some given
probability with mutateBool.
Crossover
To cross two parents, we’ll generate a bitmask that will inform us whether a given gene should be taken from the first parent or the second parent:
-- recombine two individuals from the population
crossover :: BinaryInd -> BinaryInd -> GAContext BinaryInd BinaryInd
crossover (BI i1) (BI i2) = do
-- get the crossover rate
Config{crossoverRate} <- ask
-- get a random double
indp <- randomD
if indp < crossoverRate then do -- perform crossover
-- get booleans specifying which gene to take
code <- replicateM (length i1) randomBool
-- choose genetic material from first or second parent
let eitherOr = (\takeThis this that -> if takeThis then this else that)
-- perform uniform crossover
return . BI $ zipWith3 eitherOr code i1 i2
else do
-- choose the genetic material from one of the parents
chooseFirstParent <- randomBool
return . BI $ if chooseFirstParent then i1 else i2This type of crossover is called uniform crossover.
Selection
Our selection scheme is simple: take the best 20% of the population:
select :: Ord a => Vector a -> GAContext a (Vector a)
select pop = do
-- get the population size
Config{popSize} <- ask
-- get the number of individuals to breed
let numToSelect = round $ 0.2 * (fromIntegral popSize)
-- get the top 20% of the best-performing individuals
let selectedParents = V.take numToSelect . V.reverse $ V.modify sort pop
return selectedParentsOptimizing our bit string
Almost there! It’s time to run the genetic algorithm in our main
function by instantiating a GAConfig with the functions we’ve defined:
import qualified BinaryInd as BI
main :: IO ()
main = do
let cfg = Config {
mutationRateInd = 0.8
, mutationRateGene = 0.02
, crossoverRate = 0.7
, popSize = 100
, mutate = BI.mutate
, crossover = BI.crossover
, randomIndividual = BI.new
, selectionMethod = BI.select
, fitness = BI.score
, numGenerations = 200
, hofSize = 1
, logFunc = logHOF
}
-- run the genetic algorithm
(finalSnapshot, progress) <- evalGA cfg
-- output the best fitnesses as they're found
mapM_ (putStrLn . T.unpack) progressWe call the evalGA function on our configuration to yield the final
snapshot containing the hof. We can log the progress of the genetic
algorithm by printing the logging messages written with tell and
logFunc.
The logHOF function puts the scores of the HOF into CSV format for
easy graphing:
logHOF :: Ord a => GASnapshot a -> GAContext a ()
logHOF Snapshot{hof, generationNumber} = do
-- get the fitness function
Config {fitness} <- ask
-- get string representations of the best individuals
let best = map (T.pack . show . fitness) $ Heap.toList hof
-- craft the comma-separated line
let msg = [T.concat $ intersperse (T.pack ",") best]
-- log the line
tell msgAnd here we can see how the GA improves fitness across generations:
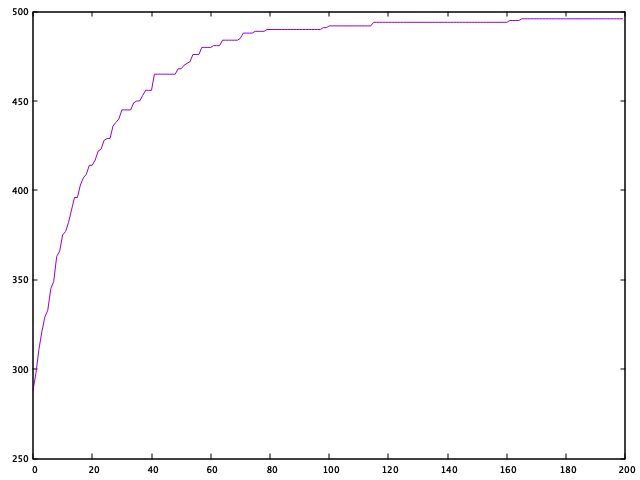
We can see that the GA is does pretty well for our little problem, making it most of the way towards an optimal solution within the first 100 generations. Not bad!
Wrapping up
We’ve prototyped a library that can allow us to see if our given (and
contrived) problem could stand to benefit from a genetic algorithm. I
realize I’ve glossed over some details here, such as the randomD and
randomBool definitions; if you want code that compiles, you’ll need to
consult the source.
I also briefly mentioned the resources for recursion schemes, but if
you’d like more examples (namely with cata, cataM, and anaM) I’ve
created a recursion-scheme-based analogue to BinaryInd in
BinaryIndRec.hs.